Views: 96

Der Kondensator im Wechselstromkreis ist ein komplexes Thema. Das in doppelter Hinsicht, da neben der Komplexität der Zusammenhänge auch das Rechnen mit komplexen Zahlen recht hilfreich ist. Auf letzteres werde ich hier aber verzichten.

Bei einem Kondensator im Gleichstromkreis ist sein Widerstand unendlich groß. Abgesehen vom Ladestrom wirkt er wie eine Unterbrechung des Stromkreises.

Fließt Wechselstrom, so lädt sich der Kondensator ständig auf und entlädt sich wieder. Die dauernde Umkehrung der Stromrichtung sorgt für einen ständigen Stromfluss. Der Kondensator nimmt Energie auf, speichert sie und gibt sie wieder ab. Bildlich gesprochen wird die Energie immer nur ohne Wirkung hin- und hergeschoben und nicht in andere Energieformen (z. B thermische) umgewandelt. Daher kommt der Begriff Blindenergie. Der Kondensator stellt im Wechselstromkreis einen Widerstand dar, der dann kapazitiver Blindwiderstand heißt.

Man kann diesen Widerstand berechnen. Im Gegensatz zum Ohmschen Widerstand, bei dem die Spannung und die Stromstärke einfließen, ist der kapazitive Blindwiderstand von der Kapazität C des Kondensators und von der Frequenz der anliegenden Wechselspannung abhängig.

Kapazitiver Blindwiderstand X_c = 1 / ωC

ω = 2πf nennt man Kreisfrequenz. Sie ist eine Kenngröße einer Wechselspannung. C ist die Kapazität des Kondensators.

Beispiel für einen Kondensator mit 1000 nF bei einer Frequenz von 50 Hz:

ω = 2πf
ω = 2π * 50 Hz
ω = 100 * π
ω = 314 s^-1

X_c = 1 / ωC
X_c = 1 / 314 * 1000 * 10^-9 [s^-1 * A * s / V]
X_c = 3175 Ω
X_c = 3,2 kΩ

10^-9 steht für „nano“.

Was bedeutet dieser Wert?

Im Kondensator wird ein (sinusförmiger Wechsel-)Strom durch eine (sinusförmige Wechsel-)Spannung begrenzt. Zusätzlich wird dadurch eine Phasenverschiebung zwischen Strom und Spannung erzeugt. Der Strom „eilt“ der Spannung voraus.

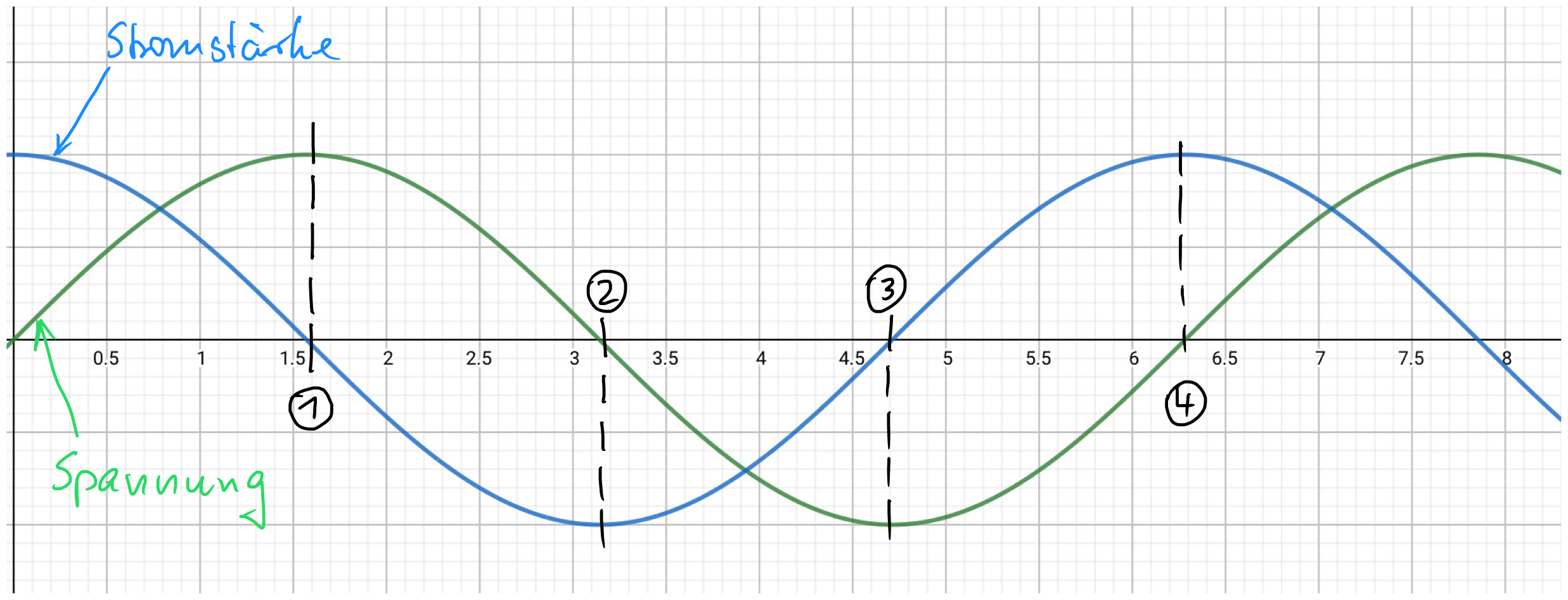
Die Beschriftung der waagerechten Achse spielt keine Rolle und soll unbeachtet bleiben.

1. Bis zum Punkt 1 fällt die Stromstärke. Gleichzeitig steigt die Spannung. Um den Kondensator zu laden, muss der Strom die Ladungsträger „hineintransportieren“. Dadurch entsteht zwischen den Kondensatorplatten eine Spannung. Da bei 1 kein Strom mehr fließt, hat die Spannung ihr Maximum.
2. Es folgt der Entladevorgang. Die Stromstärke fällt weiter bis zu ihrem Minimum, bis der Kondensator entladen ist und demzufolge die Spannung Null ist.
3. Die Stromstärke nimmt wieder zu und lädt den Kondensator. Allerdings ist er jetzt „anders herum“ aufgeladen, die Polung ist vertauscht. Sobald die Stromstärke bei Null angekommen ist, hat die Spannung erneut ein Extremum. Streng mathematisch ist es ein Minimum, praktisch ein Maximum mit umgekehrter Polung.
4. Der Strom steigt auf sein Maximum und entlädt dabei den Kondensator erneut. Damit sind wir wieder am Anfang.

Mein ehemaliger Physik-Professor würde mir jetzt sicher erklären, dass diese Erläuterung nicht ganz korrekt ist. Eine ganz streng korrekte Erläuterung würde nur leider ein Großteil nicht verstehen.

Die Stromstärke hat ihr Maximum eher als die Spannung. Das nennt man Phasenverschiebung.